Hi, all!
I'm just back from the NCTM National Meeting in Boston, where I promoted the Lab Gear, and attended a few sessions. Some of the sessions were great, and I'll be blogging about them.
One nice thing about NCTM was the opportunity to connect with friends and colleagues who I don't see often enough. Another is running into fans of my work, which happened with some regularity. My fans are few, but they're enthusiastic, and seeing them in person is a reminder that my work in curriculum development and teacher training is actually worth doing.
I was talked into joining Twitter, where I'm @hpicciotto. As the maître d' in a restaurant might say: follow me!

Summer workshop news: participants in my summer workshops will be able to get Continuing Education Units from the Rossier School of Education at the University of Southern California. This applies to the workshops in Seattle as well as the ones near Boston. Find more about my workshops at the end of this newsletter, and even more on my Web site.
Blog Posts
Here are links to posts on my Math Education Blog that you might find interesting.
If you are so moved, you may comment on the posts, and/or subscribe to the blog.
Mathematics for Equity
Mathematics for Equity is a great new book co-edited by a team consisting of two researchers from UC Berkeley School of Ed and two math teachers from the fabled "Railside" public high school. The book consists of chapters that look at high school math through various lenses, and cumulatively present a deep and multidimensional analysis of an exceptionally successful program. I was honored that the cover photo features the Lab Gear! Read my review.
Square Pairs
At some point in the early 1990's, I came across this problem: "Arrange the whole numbers from 1 to 18 into nine pairs, so that the sum of the numbers in each pair is a perfect square." I included it somewhere in my Algebra: Themes, Tools, Concepts book, and pretty much forgot about it.
A few months ago, I was asked to make a presentation on building a problem-solving culture for the San Francisco Math Circle leaders. For some reason, I started thinking about this problem again. My thinking moved in two directions: what is the best way to introduce the problem? What is the best way to extend it? Over the next period of time I got to know a lot more about the problem, in part because I thought hard about it, and in part because I got help from several talented people. Find out more about this story here, and in the subsequent post.
Logarithms
Logarithms are a notoriously difficult concept, which is often made even more so by an overemphasis on notation, terminology, and rules, and an underemphasis on understanding. I have had some success with the approach outlined in this blog post.
MathEducation.page
New on my Web site.
Pie Are Square
In honor of π day, I posted an animation that tries to show that the formula for the area of a circle is plausible. It is almost a proof that pie are square! Check it out here.
Pattern Blocks
I started my teaching career with ten years in K-5. That got me acquainted with a wide range of manipulatives, and I brought those with me to high school, where I taught for the next 32 years. Pattern blocks are a favorite of mine, which I included in my geometry curriculum, in my Space course, and in my Geometry Labs book (free download).

I recently introduced pattern blocks to a Math Teachers' Circle. (One of the participants created the beautiful tessellation above.)
While preparing for the workshop, I remembered some pattern block symmetry puzzles I had created three or four decades ago, and managed to find and duplicate them. Along with my slides and pattern block links, you can find those puzzles here.
Geometry of the Parabola
Many of us have misled students by claiming that changing the "a" parameter changes the shape of the parabola. A colleague suggested that this image can help make clear that is just not true, by focusing on a finite part of the parabola:
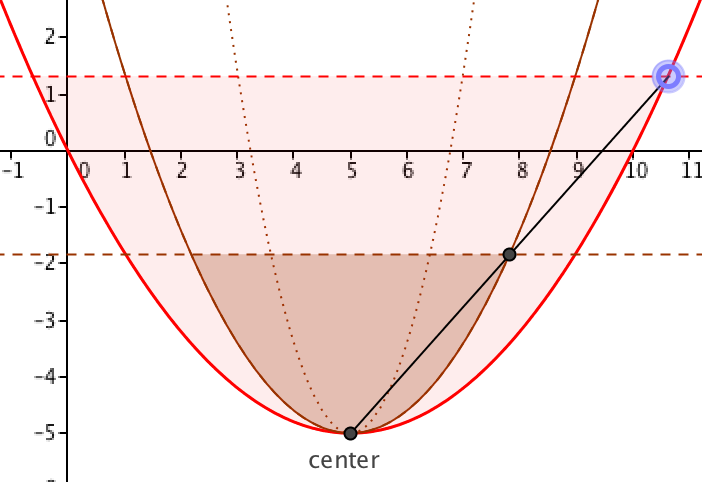
I have long had a page on the geometry of the parabola on my site, in which I explain in many ways that all parabolas are similar. The Common Core redefinition of "similar" makes this more relevant than ever. I incorporated my colleague's idea in the final GeoGebra applet on that page. The page also includes the geometric definition of the parabola, construction ideas, a proof of the reflection property, and a link to a proof that the parabola is indeed a conic section. Check it out!
