I'm just back from the California Math Council annual meeting at Asilomar. I enjoyed hanging out with my ex-colleagues, running into friends, and meeting the occasional fan of my Web site or tweets. Not to mention the chance to take a walk along the Pacific Ocean.
I think I have attended this conference every year since 1984, often as a speaker, but this time, it was extreme: I presented three times. Read about it here.
Anyway, now that it's over, I have time to put this newsletter together.

Blog Posts
Here are links to posts on my Math Education Blog that you might find interesting.
If you are so moved, you may comment on the posts, and/or subscribe to the blog.
Expository Writing for Math Students
Writing about mathematical ideas can help students strengthen their understanding. However, as it turns out, the sort of essay writing they learn to do in humanities classes is not well suited to this purpose. Nor is the ultra-concise style of mathematical proofs appropriate. It is helpful to learn from the approaches used by technical writers, the people who create users' manuals and software documentation. I got this idea from the "Railside" teachers, and further information from technical writers I know. The result is this post.
Fads and Memes
In the previous issue of this newsletter, I mentioned a blog post on teacher eclecticism. The post was very popular among teachers, but it did generate some pushback on Twitter. Part of my response to this pushback is in this post on fads and memes. Fads will always be with us. They are often originated by people who want to help teachers, but don't want to be teachers. In my view, many if not most fads have a bit of truth in them, and I have learned a lot from them over the years. Likewise, teacher-initiated memes, while they are not usually as pretentious, can be very helpful. The main thing is to not expect universal answers from any one fad or meme. (Remember: Nothing Works!)
Partitions
Marilyn Burns inspired me to explore this problem: "How many ways can you write a positive integer n as a sum of three or fewer positive integers?" I tell the story of this exploration, and the lessons it taught me, here.
MathEducation.page
New on my Web site.

Transformational Proof
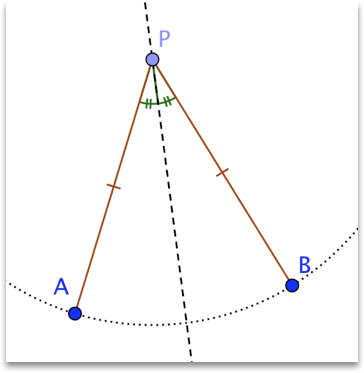
Lew Douglas and I are continuing to build a logical framework for transformational geometry in high school. We made substantial progress in the past few weeks with an approach to special triangles and quadrilaterals based on symmetry, transformations, and construction. This extends the work we started with our article on triangle congruence and similarity.
See also my epic proof of the fact that given any two congruent figures in the plane, one is the image of the other in a single reflection, rotation, translation, or glide reflection. (The presentation of the proof includes interactive figures!)
All this can be found in the For Teachers and Curriculum Developers section of my Transformational Geometry page.
Giant Pattern Block Dodecagons!
I have had my students make regular dodecagons with pattern blocks throughout my 42-year career, Kindergarten to 12th grade. But this fall, I came across a double-dimensions, quadruple-area dodecagon, and had a great time exploring it. The result was an abundantly illustrated page on my site, including beautiful contributions from fellow pattern block devotees in Michigan, Spain, and France. I also included some questions about the underlying math, which may work well with your students. Check it out!
Map Coloring
Decades ago, when I taught elementary school, one of my favorite lessons involved leading students to a discovery of the Two-Color Theorem. You never heard of it? See if you can discover it yourself, using the worksheets I created to share at NCTM last spring. (This version is aimed at secondary school students, but it was a hit with teachers at NCTM.)