If a concept is important, we should teach it more than once, and preferably in more than one way. Rate of change is important! Is there anything to add to the oft-repeated "rise over run" mantra? Yes! Whether you're teaching middle school, or calculus, or anything in between, you should be able to find some useful ideas by clicking these links.
- A puzzle based on an unsolved problem: No Three on a Line. Probably usable in upper elementary school.
- A geoboard lesson in Geometry Labs 10.2 (possibly preceded by 10.1).
- Lessons in Algebra: Themes, Tools, Concepts (ATTC), especially in chapter 8. Here is a list of all the relevant lessons: 2.9, 3.8, 4.4, 4.5, 4.8, 4.11, 5.C, 6.8 , 8.1-8.A, 8.8, 8.9, 9.2, 9.A, 9.C, 10.3, 10.6, 10.8, 11.3, l2.A, 12.5, 12.8. Many involve “real world” scenarios and multiple representations.
- Some of the ATTC lessons involve function diagrams. Go to the Function Diagrams home page for a lot more along those lines, including a lesson about operations for middle school, all the way to a visual explanation of the chain rule. Once you get the basic idea, see also Kinesthetic Function Diagrams.
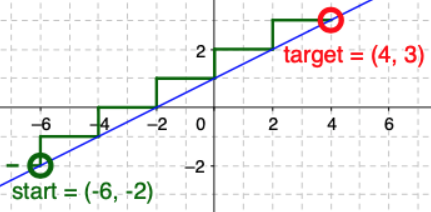
- Slope triangle puzzles in a fun applet: Stairs. (See image above.)
- Make These Designs using `y = mx + b` in an electronic grapher. One of the most popular lessons I've ever created.
- A different visualization of rate of change in a set of related applets, culminating in a challenging set of exercises: Doctor Dimension.
- "Slope Angles", an introduction to trigonometry in Geometry Labs. Do Lab 11.2 before 11.1.
- Pattern Block Trains — starts easy, gets quite challenging.
- For teachers and math nerds: formal proof of `y = mx + b` using basic geometry.